This problem has been solved!In probability theory, the expected value of a random variable, denoted or , is a generalization of the weighted average, and is intuitively the arithmetic mean of a large number of independent realizations of The expected value is also known as the expectation, mathematical expectation, mean, average, or first momentExpected value is a key concept in economics, finance, and manyY=e^x Loading y=e^x y=e^x Log InorSign Up y = e x 1 y = k

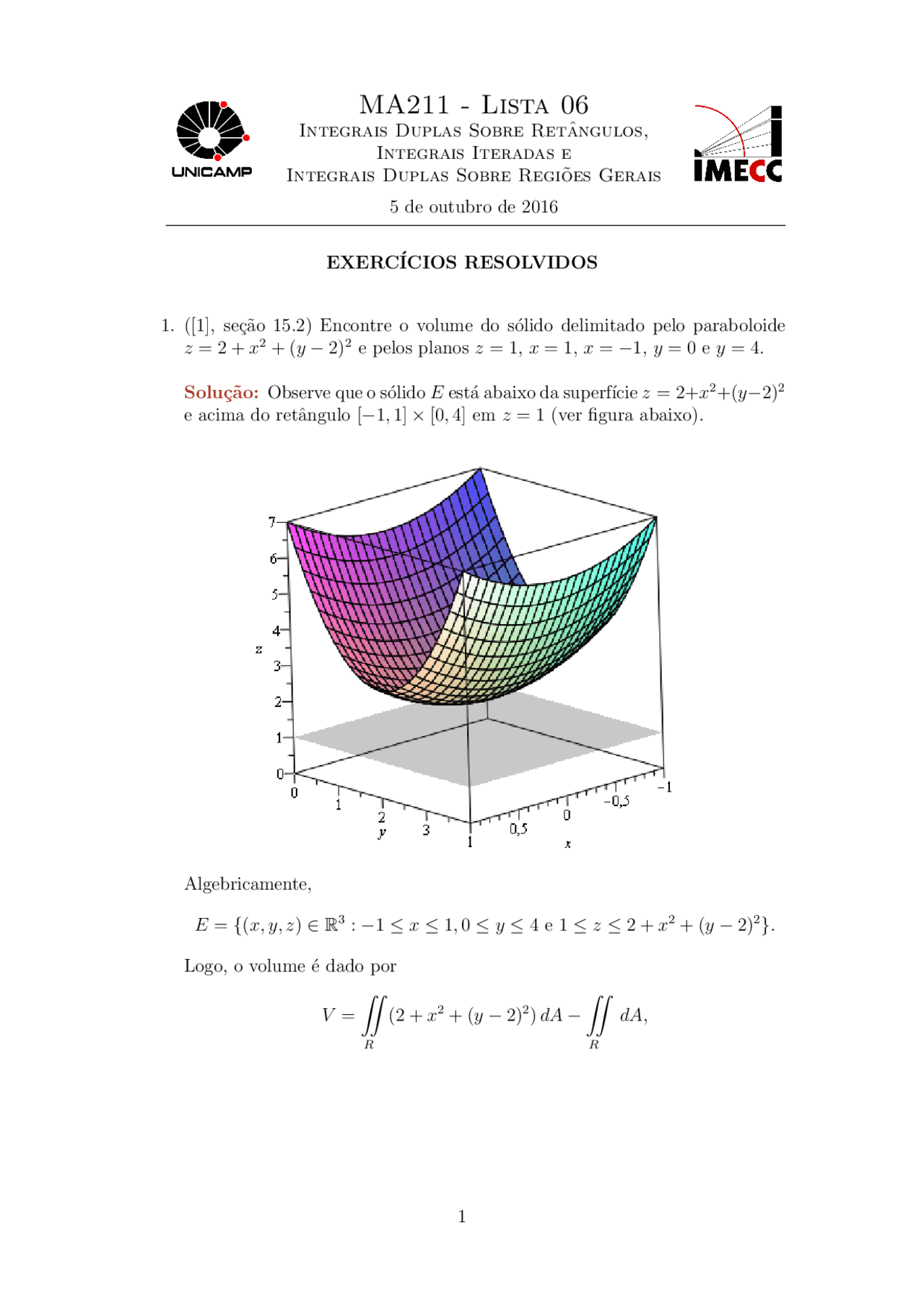
A Sketch The Graph Of Y Ex As A Curve In R2 B Sketch The Graph Of Y Ex As A Surface In R3 C Describe And Sketch The Surface Z Ey Study Com