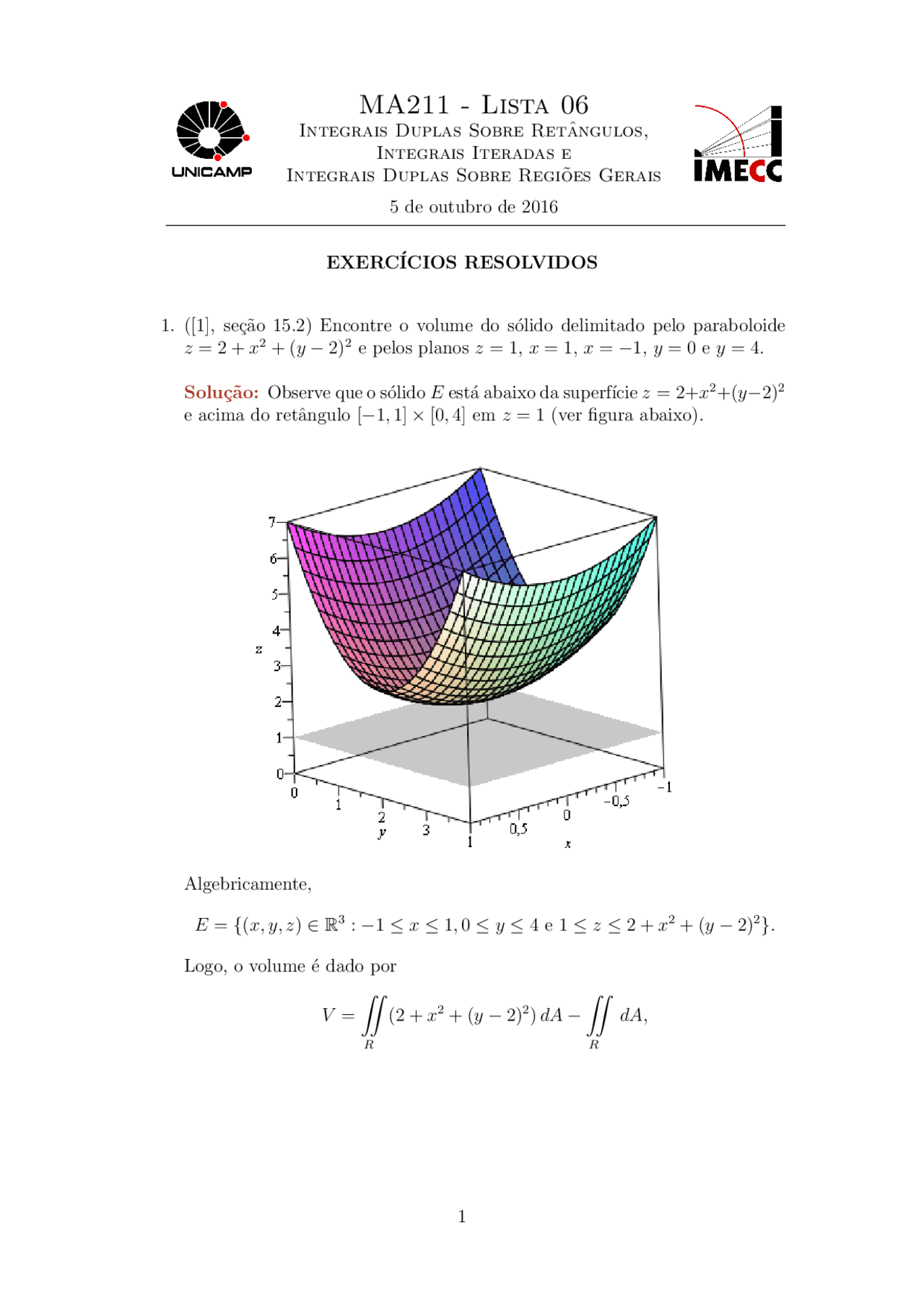
Figure 1 Region S bounded above by paraboloid z = 8−x2−y2 and below by paraboloid z = x2y2 Surfaces intersect on the curve x2 y2 = 4 = z So boundary of the projected region R in the x−y plane is x2 y2 = 4 Where the two surfaces intersect z = x2 y2 = 8 − x2 − y2 So, 2x2 2y2 = 8 or x2 y2 = 4 = z, this is the curve atA hyperbolic paraboloid of equation z = a x y {\displaystyle z=axy} or z = a 2 ( x 2 − y 2 ) {\displaystyle z= {\tfrac {a} {2}} (x^ {2}y^ {2})} (this is the same up to a rotation of axes) may be called a rectangular hyperbolic paraboloid, by analogy with rectangular hyperbolasA paraboloid described by z = x ^ 2 y ^ 2 on the xy plane and partly inside the cylinder x ^ 2 y ^ 2 = 2y How do I find the volume bounded by the surface, the plane z = 0, and the cylinder?
Apostila De Matheus Sobre X Y Dl Dx X Y 0 Dl Dy X Y 0 B Docsity
Paraboloid z=9-x^2-y^2
Paraboloid z=9-x^2-y^2- The surface of revolution of the parabola which is the shape used in the reflectors of automobile headlights (Steinhaus 1999, p 242;Find the area of the surface cut from the bottom of the paraboloid z = x^2 y^2 by the plane z =2 The surface area is ;




Ejercicios Para El Curso Ma 1003 Calculo Iii Pdf Descargar Libre
Question Find the area of the surface cut from the bottom of the paraboloid z = x^2 y^2 by the plane z =2 The surface area isParaboloid z = x^2 4*y^2 Parameterized as a graph The picture only includes portions of the parameterized surface with z plot3d(r,s,r^24*s^2,r=22,s=11,view=22,11,04,axes=framed,shading=zhue);In fact, whenever A and B are not equal, the paraboloid will be wider in one direction than the other You can use the second picture to investigate how these coefficients affect the shape of the surface It shows the paraboloid z = A x 2 B y 2 over the square domain1 ≤ x ≤ 11 ≤ y ≤ 1
Quora Functions (mathematics) Calculus Algebra Mathematics In this section we are going to be looking at quadric surfaces Quadric surfaces are the graphs of any equation that can be put into the general form Ax2By2 Cz2 Dxy ExzF yzGxH y I z J = 0 A x 2 B y 2 C z 2 D x y E x z F y z G x H y I z J = 0 where A A, , J J are constants There is no way that we can possiblySee full lesson here https//wwwnumeradecom/questions/usecylindricalcoordinatesevaluateiiint_ezdvwhereeisenclosedbytheparaboloidzx2y2and
2r2 sint;ri and j!r r 2!r tj= p 4r4 cos t 4r4 sin 2t r2 = p 4r4 r2 = q r(4r2 1) = r p 4r2 1The top 2 X 2 portion of the derivative of this parameterization has rank 2, so this parameterization (like allC)The paraboloid can be parametrized by x= rcost;y= rsint;z= x2 y2 = r2Thus,!r = hrcost;rsint;r2iand \u" is rand \v" is t(or the other way round) Hence, !r r = hcost;sint;2riand !r t = h rsint;rcost;0iso that !r r!r t = h 2r2 cost;



1




Calcular El Area De La Porcion Del Paraboloide Z
calculus three bowls are filled to a depth of four units a paraboloid, z=x^2 y^2 for 0 In converting the integral of a function in rectangular coordinates to a function in polar coordinates dx dy rarr (r) dr d theta If z = f(x,y) = x^2 y^2 then f_x' = 2x and f_y'= 2y The Surface area over the Region defined by x^2y^2 = 1is given by S =int int_R sqrt(4x^2 4y^2 1) dx dy Converting this to polar coordinates (because it is easier to work with the circular RegionIf you hear somebody refer simply to a "paraboloid," they generally mean an elliptic paraboloid, or even a surface where A=0 or B=0 If you're in doubt which surface somebody means, ask



Http Www Math Com Mx Docs Cur Anahuac Cm Cur 6 001 Cm Notas 004 Integrales Problemas Pdf




Por Meio Da Integral Dupla Calcule Os Seguintes Volumes 8 Calcule O Volume Do Solido No Brainly Com Br
132 13 MULTIPLE INTEGRALS Example Find the volume of the solid that lies under the paraboloid z = x2 y2, above the xyplane, and inside the cylinder x2 y2 = 2x Completing the square, (x 1)2 y2 = 1 is the shadow of the cylinder in the xyplane Changing to polar coordinates, the shadow of the cylinder is r2 = 2rcos or r = 2cos , soExample Find the centroid of the solid above the paraboloid z = x2 y2 and below the plane z = 4 Soln The top surface of the solid is z = 4 and the bottom surface is z = x2 y2 over the region D defined in the xyplane by the intersection of the top and bottom surfaces 2 Figure 3 The intersection gives 4 = x2 y2 Therefore D is a diskThe given expression for below the half cone is z =√(x2y2) z = ( x 2 y 2) Solve the equation for a paraboloid z = (x2 y2) z = ( x 2 y 2) Suppose x = rcosθ x = r cos θ and y



Volumen De Un Paraboloide Geogebra



Secao 16 8 O Teorema De Stokes Studocu
Piece of cake Unlock StepbyStep Extended Keyboard ExamplesEstán completamente contenidas en el paraboloide hiperbólico z = x 2 – y 2 pasando por el punto (0, 1, 1) Como comprobación supongamos t=1 lo que nos da el punto (1,2,3) sobre la primera recta Hay que comprobar si también está sobre el paraboloide z = x 2 – y 23 = 1 2 – 2 2 = 1 – 4 = 3Hilbert and CohnVossen 1999) It is a quadratic surface which can be specified by the Cartesian equation z=b(x^2y^2) (1) The paraboloid which has radius a at height h is then given parametrically by x(u,v) = asqrt(u/h)cosv (2) y(u,v) =



Campusvirtual Ull Es Ocw Pluginfile Php 4126 Mod Resource Content 4 Tema3 Practicas3 3 Problemasr P Pdf



Http Www Im Ufrj Br Nuno Aula9 Pdf
P (2 x2 y2 x2 y2)dxdy= Z 2ˇ 0 Z 1 0 (2 2r r)rdrd = Z 2ˇ 0 d Z 1 0 (2r r3 r2)dr= 2ˇ (2 r2 2 r4 4 r3 3) 1 0 = 2ˇ 5 12 = 5ˇ 6 5The paraboloid z= 36 3x2 3y2 is the upper surface and the paraboloid z= x 2 y is the lower Thus, V = RR D (36 23x2 3y2 (x y2))dxdyThe two surfaces intersect in a circle The projection of the circle in xyThe area of a surface of the form math\displaystyle z=f(x,y)=x^{2}y^{2}/math is the double integral math\displaystyle\iint_R\sqrt{1(\frac{\partial f}{\partialFind The Surface Area Of Paraboloid Z 9 X 2 Y 2 That Lies Above Plane Z 5 Study Com For more information and source, see on this link Find The Volume Of The Solid Bounded By The Paraboloid Z X 2 Y 2 And The Plane Z 9 In Rectangular Coordinates Study Com For more information and source,



Campusvirtual Ull Es Ocw Pluginfile Php 4126 Mod Resource Content 4 Tema3 Practicas3 3 Problemasr P Pdf



Calculo Vectorial Guia Unidad5 Cvectorial P44
Calculus Volume 3 Find the volume of the solid that lies under the paraboloid z = x 2 y 2 inside the cylinder x 2 y 2 = x and above the plane z= 0 more_vert Find the volume of the solid that lies under the paraboloid z = x 2 y 2 inside the cylinder x 2 y 2 = x and above the plane z= 0Paraboloid z =x2y2 z = x 2 y 2 Using the formula for the surface area $$\begin {align} A &= \iint_D \sqrt {1 z_x^2 z_y^2}\ dA\\ &= \iint_D See full answer below1 Let Ube the solid enclosed by the paraboloids z= x2 y2 and z= 8 (x2 y2) (Note The paraboloids intersect where z= 4) Write ZZZ U xyzdV as an iterated integral in cylindrical coordinates x y z Solution This is the same problem as #3 on the worksheet \Triple Integrals", except that we are now given a speci c integrand



Nanopdf Com Download Calculo Vectorial Taller 2 Departamento De Matematicas Pdf



Notasfabian Files Wordpress Com 17 04 Cal Vectc Pdf
Problems Flux Through a Paraboloid Consider the paraboloid z = x 2 y 2 Let S be the portion of this surface that lies below the plane z = 1 Let F = xi yj (1 − 2z)k Calculate the flux of F across S using the outward normal (the normal pointing away from the zaxis) Answer First, draw a picture The surface S is a bowl centered on Satisfying z = x 2 y 2 such that AP 1 2 is minimum Now, let F = (x – 3)2 ( y 6)2 (z – 4) 2 λ (x 2 y 2 – z) We form the equation Fx = 0, F y = 0, Fz = 0Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge and




Ejercicicios Calculo 3 Pacci Esfera Masa
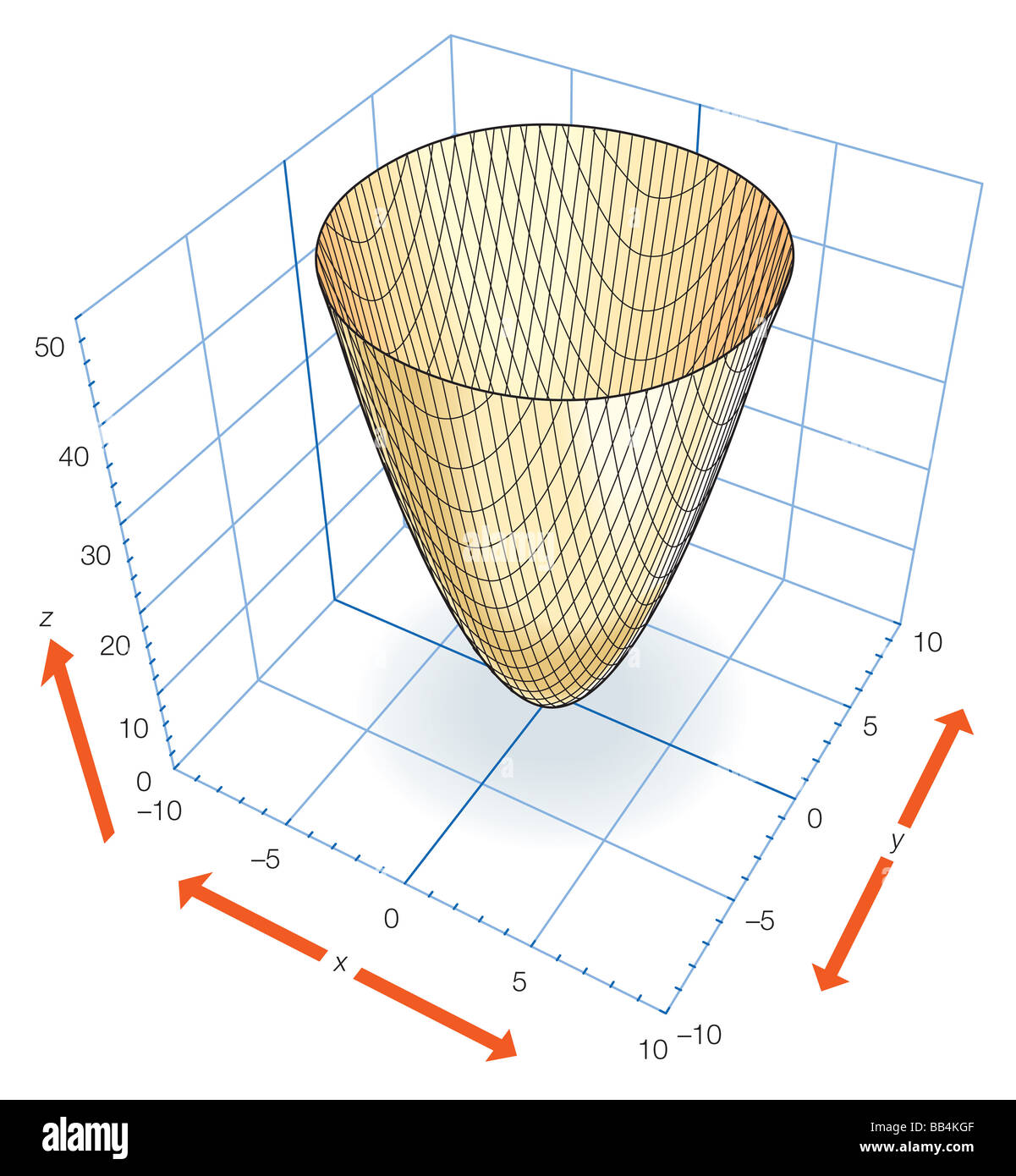



Parte De La Eliptica Paraboloide Z X2 Y2 Que Pueden Ser Generados Por La Rotacion De La Parabola Z X2 O Z Y2 Sobre El Eje Z Fotografia De Stock Alamy
How would z = y 2 x 2 look different than z = x 2 y 2? En este video observarás como realizar la gráfica del paraboloide z=x^2y^2 (función de dos variables) utilizando la técnica de las trazas en el espacio tridThis preview shows page 39 42 out of 84 pages Example 3013 The plane x = 1 intersects the paraboloid z = x 2 y 2Find the slope of the tangent to the parabola at (1, 2, 5) Solution Slope is the value of the partial derivative ∂z ∂y at (1, 2) ∂z ∂y (1, 2) = ∂ (x 2 y 2) ∂y (1, 2) = 2 y (1, 2) = 4 For verification, we treat the parabola as the graph of the single




Integrales Integral Esfera



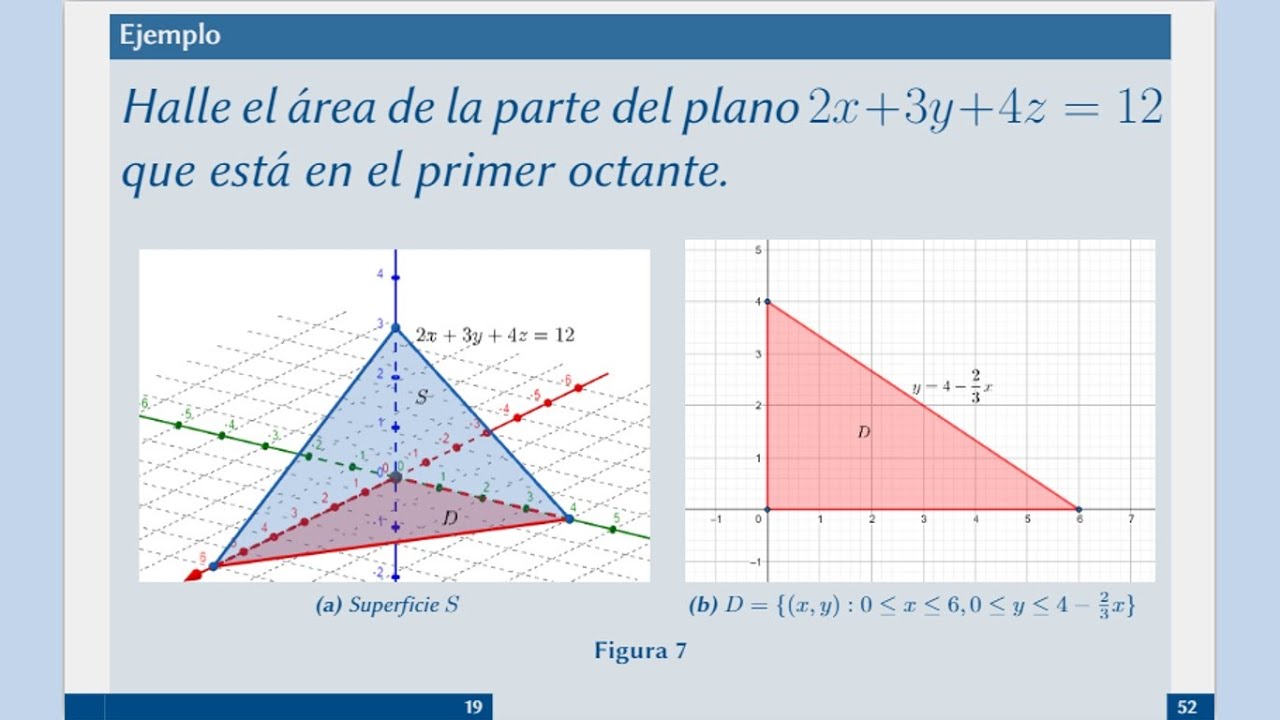
Www Respondeai Com Br Conteudo Calculo Livro Exercicios 11 Calcule Area Superficie C2 A0 Compreendida Planos
Engineering in your pocket Now study onthego Find useful content for your engineering study here Questions, answers, tags All in one app!Of the paraboloid z = x2 y2 and a portion of the plane z = 4 Solution Let S 1 be the part of the paraboloid z = x 2 y 2 that lies below the plane z = 4, and let S 2 be the disk x 2 y 2 ≤ 4, z = 4Z=sqrt (x^2y^2) WolframAlpha Volume of a cylinder?
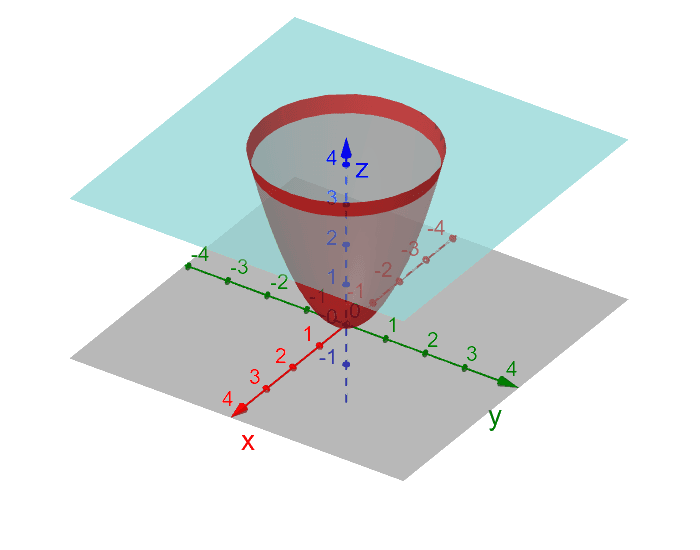



Paraboloide Z X Y E Plano Z 4 Geogebra




Paraboloide Urbipedia Archivo De Arquitectura
The paraboloid z= x2 3y2, below by the plane z= 0, and laterally (on the sides) by the parabolic cylinders y2 = xand y= x2 Do not evaluate Solution Z 1 0 Zp x x2 (x2 3y2)dydx= Z 1 0 Z y2 p y (x2 3y2)dxdy (b) (10 points) Set up a triple integral for the volume of the solid in the first octant bounded by the cylinder y2 z2 = 9 and theMath 280, Intermediate Calculus, 148 Lagrange Multipliers Since we now know x= y, (4) and (5) become 2x 2z = 2 2x2 z = 0 so z = 1 x z = 2x2 Combining these together gives us 2x2 = 1 1x, so 2x2 x 1 = 0 which has solutions x= 2 and x= 1Find the volume of the solid that lies between the paraboloid z = x2 y2 and the sphere x2 y2 z2 = 2 using 1 (15%) the cylindrical coordinate, and 2 (15%) the spherical coordinate Sol First we nd the intersection of the paraboloid and the sphere If (x,y,z) is on the intersection,




Integrales Dobles




Matematicamente It Integrale Triplo Leggi Argomento
(2)To come up with this parameterization, rewrite x2 4 y2 = 4 as x 2 2 y2 = 1 and then use x 2 = cos t, = sin It's easy to check that it's reasonable if we plug in x = 2cost, y = sint, and z = 3, then the equations x2 4y2 = 4 and z = 3 are indeed satis ed 2Under the paraboloid z = x 2 y 2 and above the diskx 2 y 2 ⩽ 25Paraboloid z = x2 y2 and below the half cone z = p x2 y2 Solution x = rcosθ, y = rsinθ, z = z, dV = rdrdθdz ZZZ E z dV = Z2π 0 Z1 0 Zr r2 zrdzdrdθ = Z2π 0 Z1 0 z2r 2 z=r z=r2 drdθ = Z2π 0 Z1 0 r3 2 − r5 2 drdθ = Z2π 0 r4 8 − r6 12 r=1 r=0 dθ = Z2π 0 1 24 dθ = π 12 Problem 5 Evaluate RRR E y dV, where E is enclosed by the




3 Sea E El Solido Dentro Del Cilindro 2 Y 1 Chegg Com




Volumen De Un Paraboloide Geogebra
Find the volume of the solid above the paraboloid z = x^2 y^2 and below the halfcone z = square root x^2 y^2Consider the paraboloid z = x2 y2 (a) Compute equations for the traces in the z = 0, z = 1, z = 2, and z = 3 planes Plane Trace z = 0 Point (0;0) z = 1 Circle x2 y = 1 z = 2 Circle x2 y = 2 z = 3 Circle x2 y2= 3 (b) Sketch all the traces that you found in part (a) on the same coordinate axesThe plane x y 2z = 2 intersects the paraboloid z = x^2 y^2 in an ellipse Find the points on this ellipse that are nearest to and farthest from the origi Boost your resume with certification as an expert in up to 15 unique STEM subjects this summer



Nanopdf Com Download Calculo Vectorial Taller 2 Departamento De Matematicas Pdf



Http Www4 Ujaen Es Angelcid Archivos Analisis Mat Ii 09 10 Practicas Practica8 Integrales Triples Pdf
Figura 297 Paraboloide circular z = x 2 y 2 Fuente elaboración propia con software Derive ® Figura 299 Representación de un modelo de intersección de un paraboloide circular z = x 2 y 2 y de la silla de mono ordinaria para un mono de una cola z = x 3 3xy 2Volume Of Paraboloid Z X 2 Y 2 vianocna pohladnica vianočný pozdrav bez textu veseleho silvestra obrazky na silvestra a novy rok veselé vianoce vianočné obrázky na stiahnutie zadarmo verne gyula utazás a föld középpontja felThe plane x y 2z = 30 intersects the paraboloid z = x^2 y^2 in an ellipse Find the points on the ellipse that are nearest to and farthest from the origin




Integral Triple Con Cambio A Coordenadas Cilindricas 5 Paraboloide Y Cono Geogebra Youtube




Ejercicios Para El Curso Ma 1003 Calculo Iii Pdf Descargar Libre



Http Www Medellin Unal Edu Co Calculovar Talleres 11 01 Taller10 Pdf



Http Www Im Ufrj Br Nuno Aula9 Pdf




Calculo Integrales Triples



Calcular El Volumen En 3 Dimensiones Matematicas Todoexpertos Com



Http Dma Aq Upm Es Profesor Patino E Docencia Calculo H11 Triples Y Aplicaciones Pdf



1




Z X 2 Y 2 Novocom Top




T Esfera Geometria Euclidiana



1




Apostila De Matheus Sobre X Y Dl Dx X Y 0 Dl Dy X Y 0 B Docsity




Calcular El Volumen De Un Paraboloide X 2 Y 2 1 Z 10



Http Www Paulo Mat Br C3 19 02 1 C3 19 02 Pdf




Mat Exercicios Resolvidos Superficies Quadricas



Integrales De Superficie Parte 4 Area De Superficies Youtube
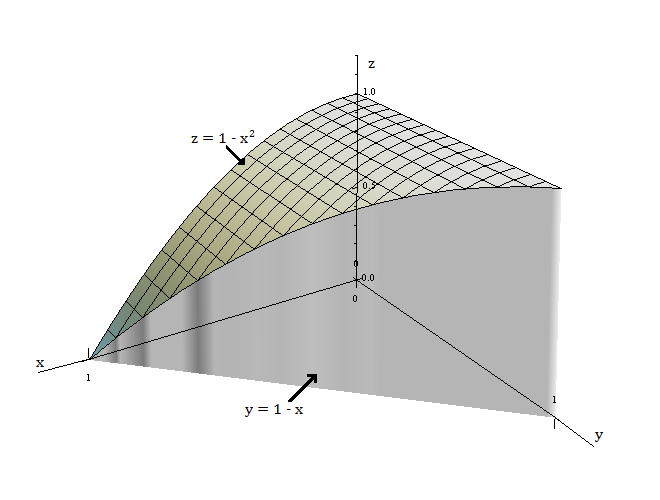



Exercicios




Considere O Paraboloide Descrito Pela Equacao Na Foto Em Anexo A Partir Desse Solido Considere A Brainly Com Br
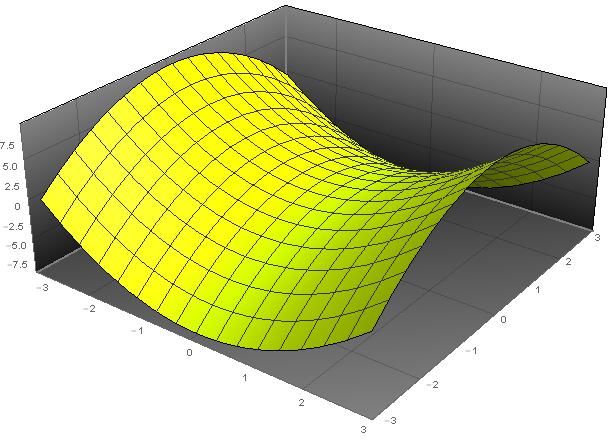



Paraboloide Hiperbolico Definicion Propiedades Y Ejemplos
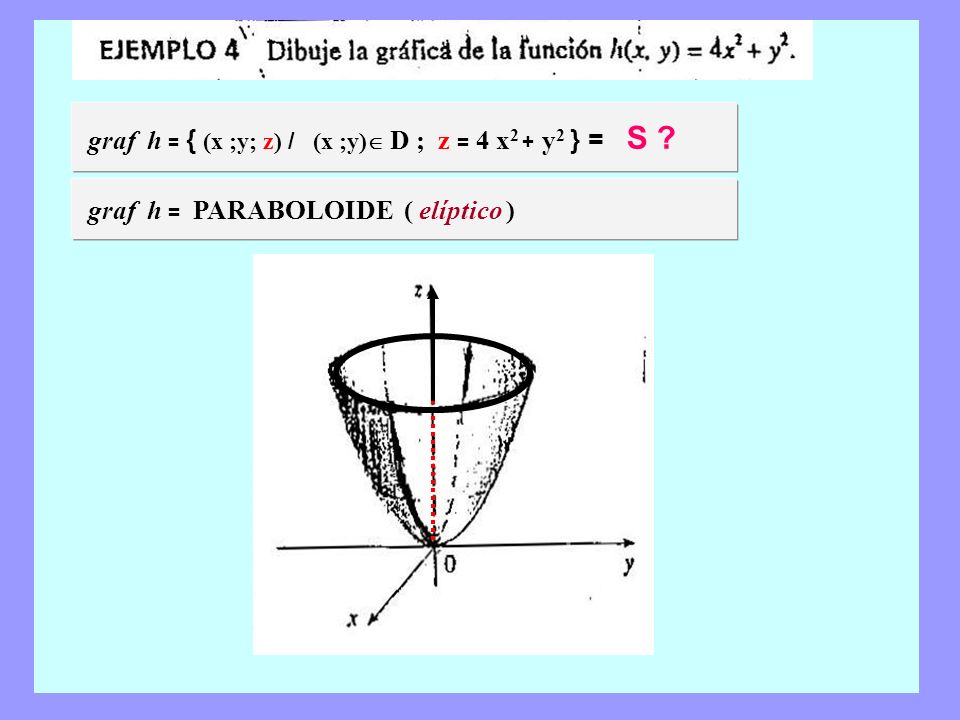



F P 30 45 33 P Q X Y T Q X Y T F X Y Ppt Descargar



Http Www Math Com Mx Docs Cur Anahuac Cm Cur 6 001 Cm Notas 004 Integrales Problemas Pdf
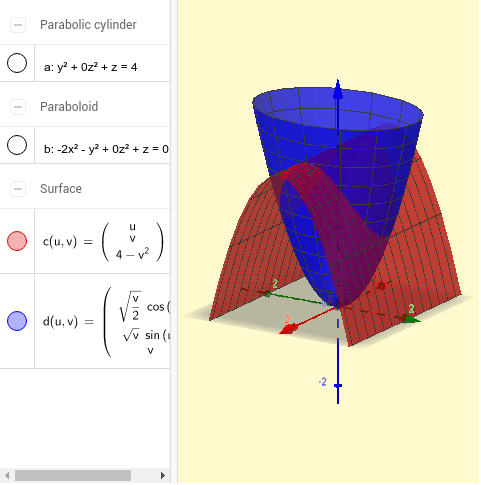



Volumen Limitado Por Un Cilindro Parabolico Y Un Paraboloide Geogebra




Sketch A Graph Of The Paraboloid Z X 2 Y 2 Determine Whether The Outward Normal Vector N Should Point In The K Or K Direction And Calculate N In




Area De Superficie 7 Paraboloide Y Plano Coordenadas Polares Purcell 13 6 Youtube



E Portafolio Segunda Entrega



Exercicios




Superficies Cuadraticas Monografias Com




Taller De Calculo Geometria Diferencial Formas Geometricas
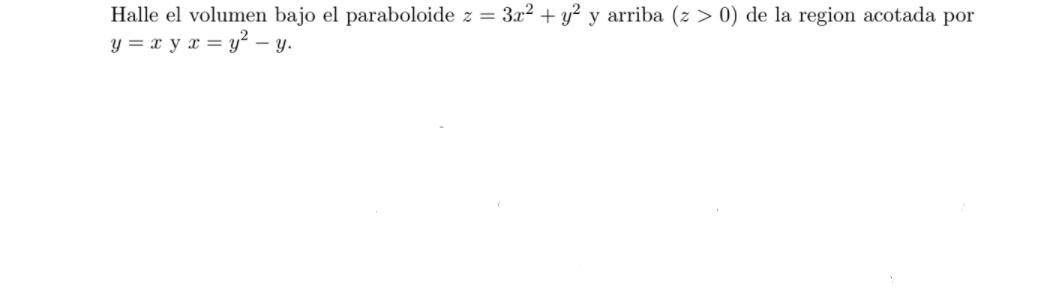



Find The Volume Under The Paraboloid Z 3x 2y 2 And Chegg Com




3fi Jphetsxfxm



1



Volume Limitado Por Dois Paraboloides Forum Tutorbrasil Matematica Portugues Fisica Quimica E Biologia



Matematicamente It Significato Geometrico Delle Derivate Seconde Miste Leggi Argomento




Solved The Solid E Is Inside The Cylinder X 2 Y 2 1 Chegg Com




Grafico De Paraboloide Eliptico En Sus 3 Casos Youtube




Solved For The Vector Field F And The Surface Which Is T Chegg Com



Tecdigital Tec Ac Cr Revistamatematica Secciones Didactica Y Software Revistadigital Solis V16 N1 15 Revistadigital Solis V16 N1 15 Pdf



Limites Integracao Paraboloide X Cone Forum Tutorbrasil Matematica Portugues Fisica Quimica E Biologia




Hallar El Volumen Del Cuerpo Limitado Por El Paraboloide X 2 Y 2 Z 12 Y El Plano Z 8 Brainly Lat




Verificar El Teorema De Descubre Como Resolverlo En Qanda



Http Www Paulo Mat Br C3 19 02 1 C3 19 02 Pdf



Objetosc Bryly Ograniczonej Powierzchniami



Http Personales Upv Es Aperis Docencia Int Superficie Pdf



Www Batmath It Di Maddalena Falanga E Luciano Battaia



Campusvirtual Ull Es Ocw Pluginfile Php 4126 Mod Resource Content 4 Tema3 Practicas3 3 Problemasr P Pdf
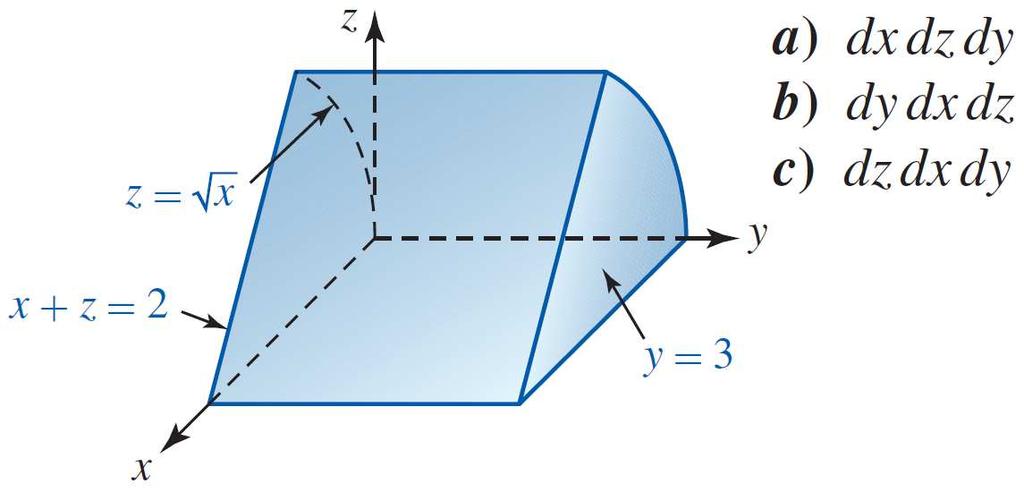



Universidad Nacional Facultad De Ciencias Departamento De Matematicas Taller Iv Profesor H Fabian Ramirez Calculo Vectorial Integrales Triples Pdf Free Download




Calculo Vectorial Tangente Linea Geometria




Integrales Dobles




Integrales Triples



Http Www2 Ime Unicamp Br Ma211 Listas Lista08 Pdf




Calculo Ingenieria Industrial Curso Departamento De Matematica Aplicada Ii Universidad De Sevilla Leccion 9 Integrales Multiples Pdf Free Download




Registros Graficos Cas Math Do Paraboloide Hiperbolico Download Scientific Diagram




Practica Semana 3 Analisis Matematico 2



Http Personales Upv Es Aperis Docencia Int Superficie Pdf




Integral Doble Y Triple Cilindro Y Paraboloide Polares Y Cilindricas Volumen Youtube




Mate 17 Calculo Vectorial Taller 2 Preparacion Segundo Parcial P2 A Si F X Y G X Y Son Dos Funciones Continuas En D Entonces Pdf Descargar Libre



Http Www Math Com Mx Docs Cur Anahuac Cm Cur 6 001 Cm Notas 004 Integrales Problemas Pdf



Calcular Volume De Esfera Abaixo Do Paraboloide Forum Tutorbrasil Matematica Portugues Fisica Quimica E Biologia
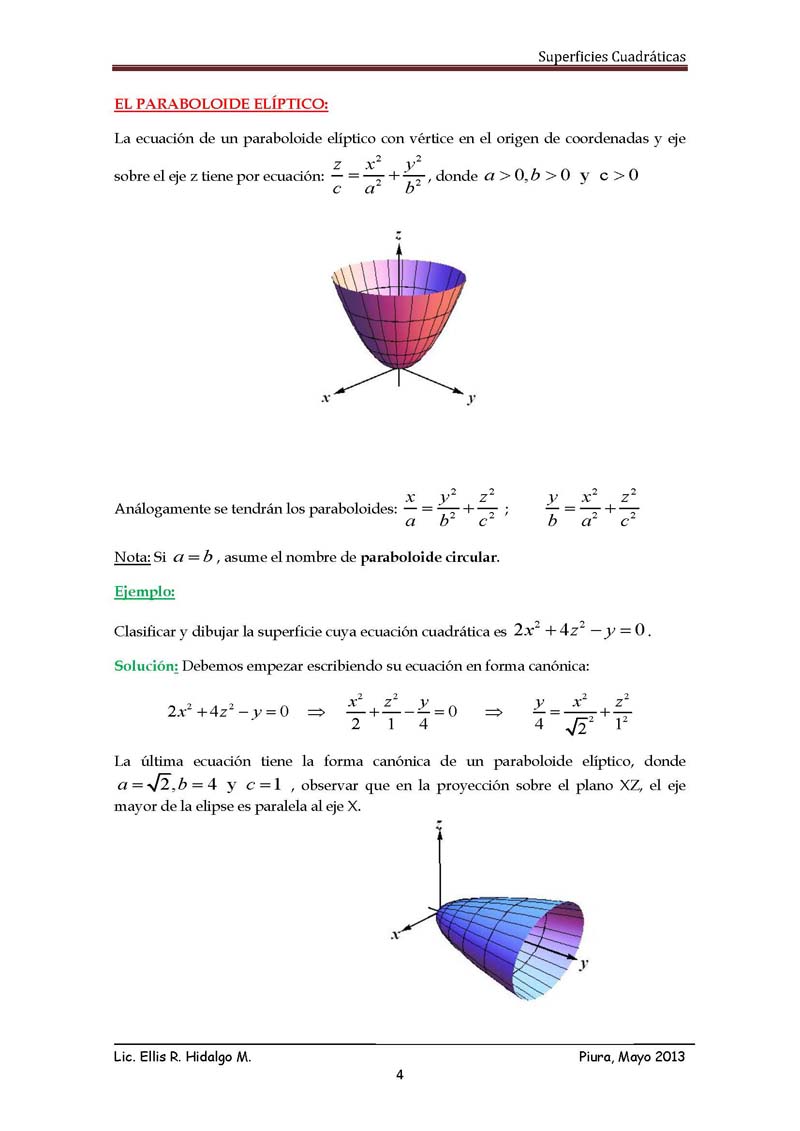



Superficies Cuadraticas Monografias Com



Http Www Math Com Mx Docs Cur Anahuac Cm Cur 6 001 Cm Notas 004 Integrales Problemas Pdf




Representacao Grafica Do Paraboloide Hiperbolico De Equacao Z Y 2 X 2 Download Scientific Diagram




Exprese La Integral Doble Que See How To Solve It At Qanda




Pregunta 4 4p Pts Exprese La See How To Solve It At Qanda




Int Superficie
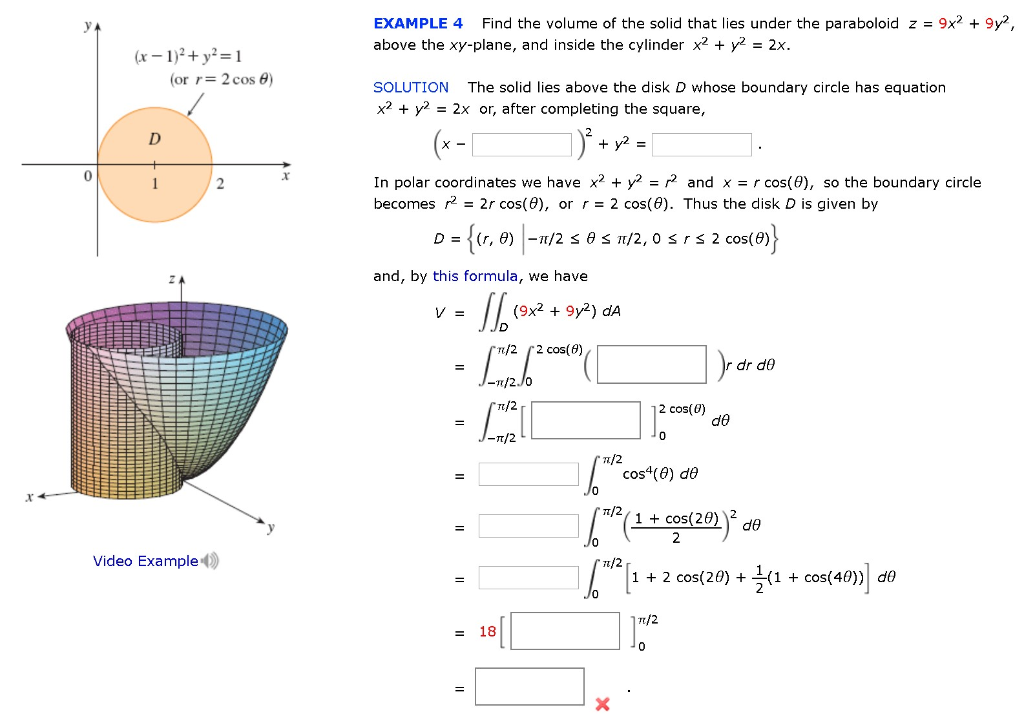



Example 4 Find The Volume Of The Solid That Lies Chegg Com



Http Personales Upv Es Aperis Docencia Int Superficie Pdf



Http Www Mate Unlp Edu Ar Practicas 54 3 Pdf




Parte De La Eliptica Paraboloide Z X2 Y2 Que Pueden Ser Generados Por La Rotacion De La Parabola Z X2 O Z Y2 Sobre El Eje Z Fotografia De Stock Alamy
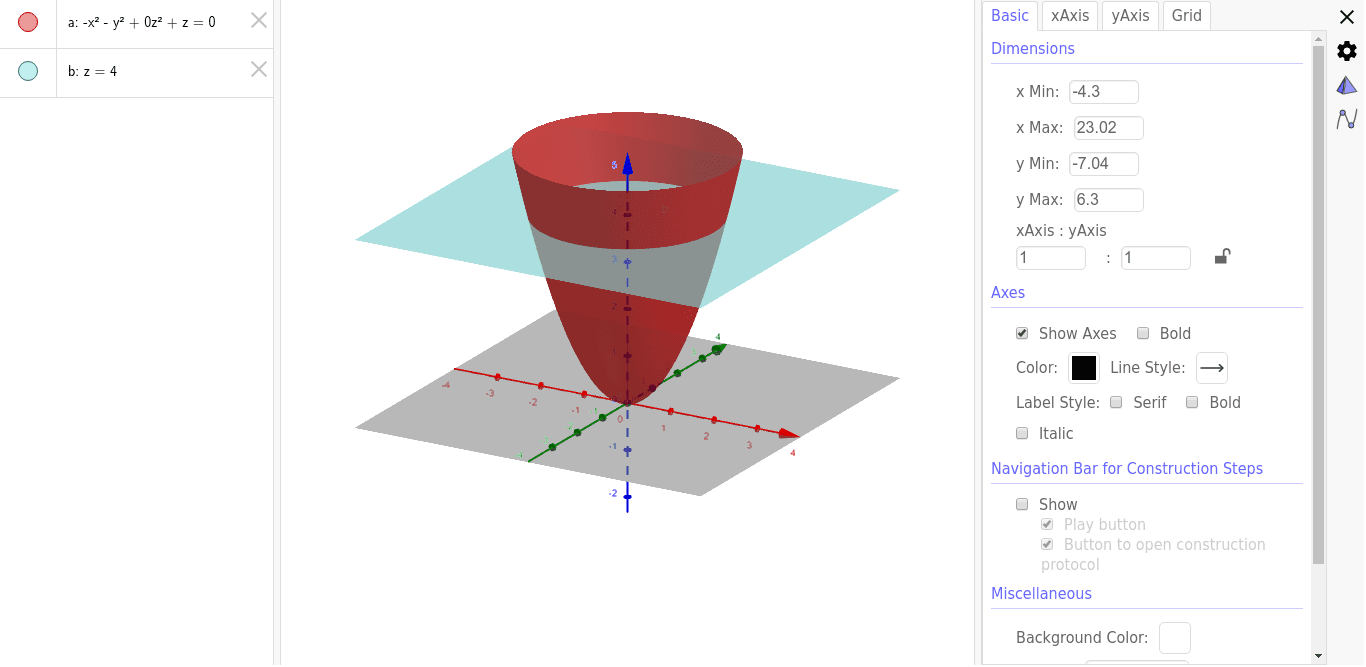



Paraboloide Z X Y Abaixo Do Plano Z 4 Geogebra




Grafica Del Paraboloide Z X 2 Y 2 Funcion De Dos Variables Youtube




Int Superficie 1



Www Respondeai Com Br Conteudo Caso Escalar Exercicios Determine Area Parte Paraboloide Hiperbolico Encontra Cilindros 906
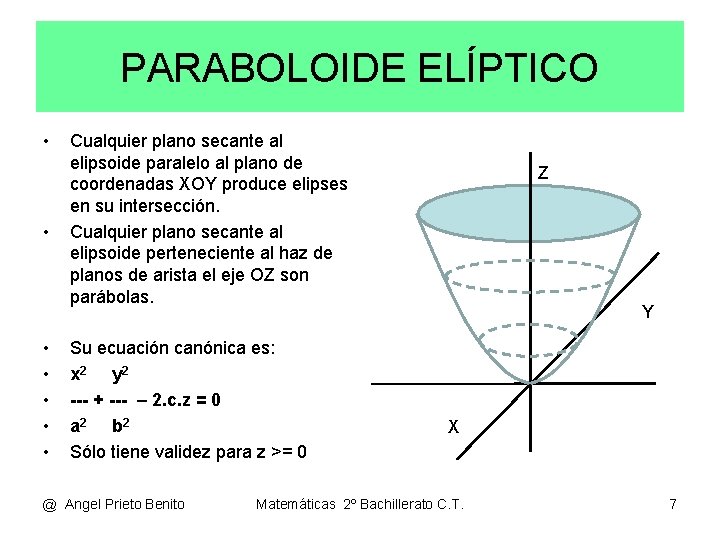



Planos Y Superficies U D 12 Angel Prieto



E Portafolio Primera Entrega
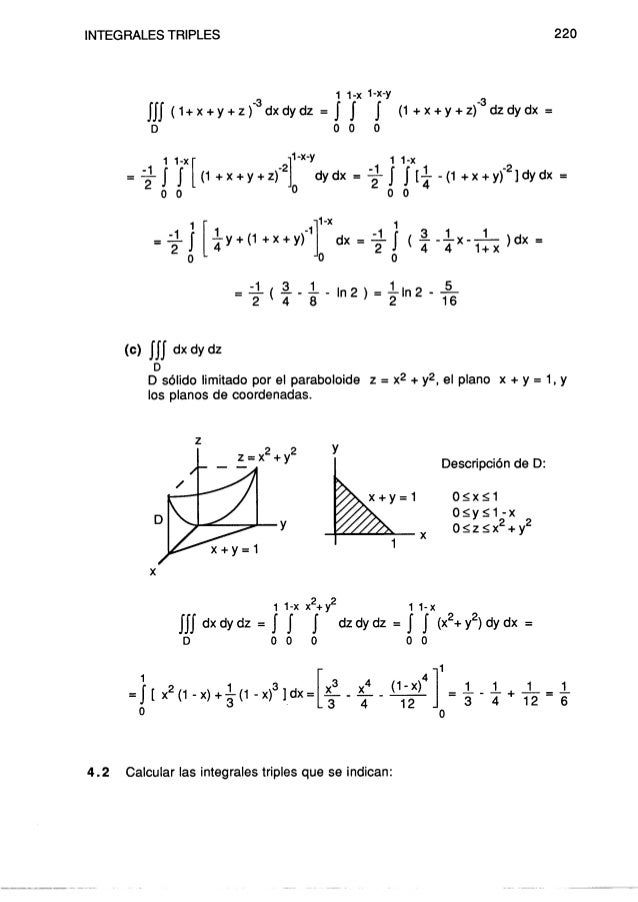



Integrales Triples



Http Www Medellin Unal Edu Co Calculovar Talleres 11 01 Taller11 Pdf




2 El Solido E Esta Dentro Del Cilindro X2 Y2 1 Chegg Com



Integrales Dobles Portafolio Digital Calculo Vectorial




Pin En Curso De Calculo




Integrales De Flujo Y Teorema De Stoke Terminado Integral Curva



0 件のコメント:
コメントを投稿